Shows a position-versus-time graph for a particle in shm. provides a window into the intriguing world of simple harmonic motion, a fundamental concept in physics that governs the rhythmic oscillations of countless systems. From the gentle sway of a pendulum to the pulsations of a vibrating guitar string, SHM plays a vital role in understanding the dynamic behavior of the universe around us.
This graph serves as a visual representation of the particle’s journey through time, capturing its position as it oscillates back and forth. It unveils the intricate relationship between displacement, velocity, and acceleration, revealing the underlying forces that drive the particle’s motion.
Simple Harmonic Motion (SHM): Shows A Position-versus-time Graph For A Particle In Shm.
Simple harmonic motion (SHM) is a periodic motion where an object oscillates back and forth along a straight line, repeating its motion at regular intervals. The motion is characterized by a sinusoidal function and is often observed in systems where a restoring force acts on the object, such as a spring or a pendulum.
Position-versus-Time Graph in SHM
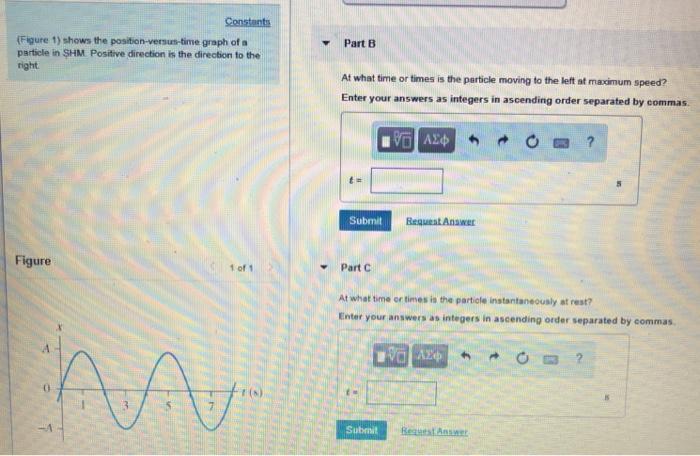
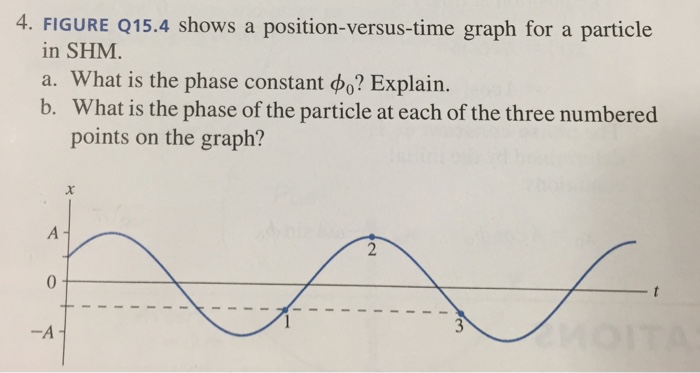
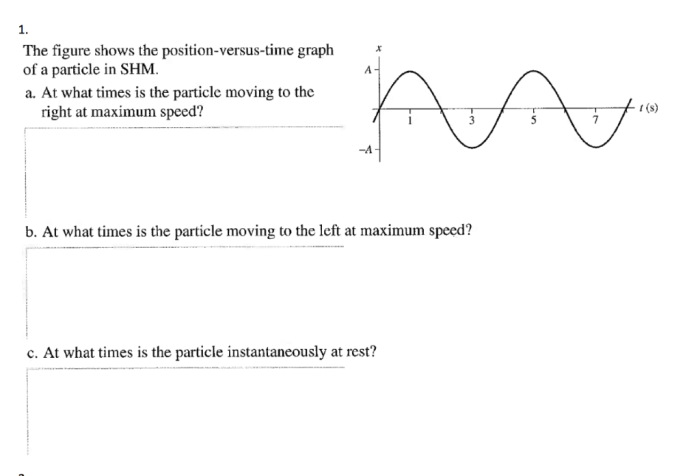
The position-versus-time graph for a particle in SHM is a sinusoidal curve. The curve represents the displacement of the particle from its equilibrium position as a function of time. The amplitude of the graph represents the maximum displacement of the particle, while the period represents the time it takes for the particle to complete one full cycle of oscillation.
Amplitude and Period
The amplitude of a SHM is the maximum displacement of the particle from its equilibrium position. The period is the time it takes for the particle to complete one full cycle of oscillation.
Frequency and Phase
The frequency of a SHM is the number of oscillations the particle makes per second. The phase is the angle at which the particle starts its oscillation.
Energy Considerations
In SHM, the particle has both potential and kinetic energy. The potential energy is stored in the system when the particle is displaced from its equilibrium position, while the kinetic energy is the energy of motion when the particle is moving.
The total energy of the system is constant and is equal to the sum of the potential and kinetic energy.
Resonance, Shows a position-versus-time graph for a particle in shm.
Resonance occurs when the frequency of an external force matches the natural frequency of a system. This causes the system to oscillate with a larger amplitude than it would at other frequencies.
Applications of SHM
SHM is a fundamental concept in physics and has many applications in various fields.
- Springs: Springs are used to store energy and release it when compressed or stretched. The motion of a spring is an example of SHM.
- Pendulums: Pendulums are used to measure time and are also an example of SHM.
- Vibrating strings: Vibrating strings are used in musical instruments to produce sound. The motion of a vibrating string is an example of SHM.
FAQ Insights
What is the significance of amplitude in SHM?
Amplitude represents the maximum displacement of the particle from its equilibrium position, providing insights into the energy stored in the system.
How does frequency relate to the period of oscillation?
Frequency is the inverse of the period, indicating the number of oscillations completed per unit time.
What is the role of phase in SHM?
Phase determines the starting point of the particle’s oscillation, providing information about its initial displacement and velocity.