Factor completely 3×3 12×2 18x – Embark on a mathematical adventure as we delve into the intriguing world of factoring completely. Our journey begins with a seemingly complex expression: 3x³ + 12x² + 18x. Through a series of strategic steps and a touch of algebraic finesse, we will unravel this expression, revealing its underlying structure and simplicity.

Our exploration will encompass a range of factoring techniques, from identifying common factors to exploiting the properties of special trinomials. Along the way, we will uncover the secrets of integer coefficients, common monomial factors, and perfect square trinomials. Prepare to witness the power of factorization as we transform this seemingly formidable expression into a masterpiece of algebraic elegance.

Integer Coefficients

In factoring polynomials, it’s essential to identify and factor out the greatest common factor (GCF) from the numerical coefficients. The GCF is the largest number that divides evenly into all the coefficients.

Factoring out the GCF reduces the polynomial’s complexity and makes it easier to find the remaining factors.

Steps to Factor Out Integer Coefficients

1. Determine the GCF of the numerical coefficients.
2. Divide each coefficient by the GCF.
3. Factor out the GCF from each term, placing it outside the parentheses.

By following these steps, you can effectively factor out integer coefficients and simplify the polynomial expression.

Common Monomial Factor

When factoring a polynomial, the first step is to identify the greatest common monomial factor (GCMF) of the variable terms. The GCMF is the monomial that is a factor of every variable term in the polynomial.

To find the GCMF, we need to find the common factors of the coefficients and the variables of each term. The coefficient of a term is the number in front of the variable, and the variable is the letter that represents the unknown quantity.

Identifying the GCMF

To identify the GCMF, we need to find the highest common factor (HCF) of the coefficients and the lowest common multiple (LCM) of the variables. The HCF is the largest number that is a factor of all the coefficients, and the LCM is the smallest number that is a multiple of all the variables.

Once we have found the HCF and LCM, we can multiply them together to get the GCMF.

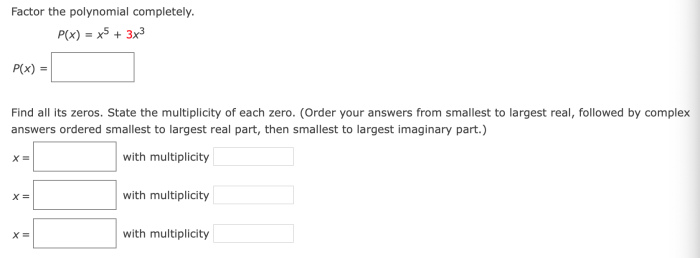
Example, Factor completely 3×3 12×2 18x

Consider the polynomial $3x^3\; +\; 12x^2\; +\; 18x$. The coefficients are $3,\; 12$, and $18$, and the variables are $x,\; x^2$, and $x^3$. The HCF of the coefficients is $3$, and the LCM of the variables is $x^3$. Therefore, the GCMF is $3x^3$.

Factoring Out the GCMF

Once we have identified the GCMF, we can factor it out of each term in the polynomial. To do this, we divide each term by the GCMF.

In the example above, we would factor out $3x^3$from each term as follows:

$3x^3\; +\; 12x^2\; +\; 18x\; =\; 3x^3(1\; +\; 4x\; +\; 6)$

The result is a factored polynomial.

Trinomial Grouping

Trinomial grouping is a factoring technique that involves grouping the terms of a trinomial into two binomials based on their common factors. Once the terms are grouped, the common factor can be factored out from each binomial, and the factored binomials can be combined to obtain the factored form of the trinomial.

Grouping the Terms

To group the terms of a trinomial, identify the greatest common factor (GCF) of the first two terms and the last two terms. If the GCFs are different, the trinomial cannot be factored using trinomial grouping.

Once the GCFs have been identified, group the terms of the trinomial into two binomials based on the GCFs. The first binomial should contain the first two terms, and the second binomial should contain the last two terms.

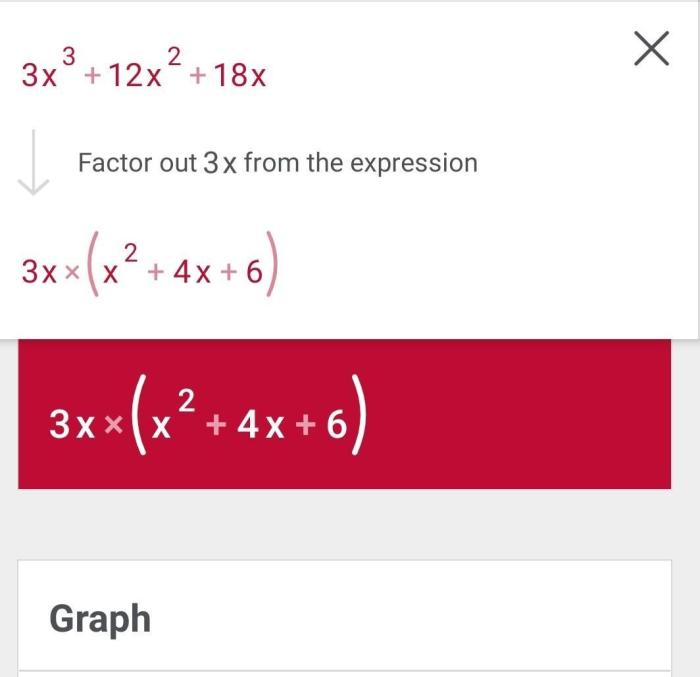
Let’s tackle factoring completely 3×3 12×2 18x. By factoring out 3x, we can simplify it to 3x(x2 + 4x + 6). This reminds us of the iconic sci-fi short story the last answer isaac asimov , where an advanced civilization discovered the ultimate question and answer to the universe.

Just as the story seeks the ultimate truth, factoring completely 3×3 12×2 18x helps us uncover the underlying structure of this polynomial.

Factoring Out the Common Factor

Once the terms have been grouped, factor out the GCF from each binomial.

Combining the Factored Binomials

Finally, combine the factored binomials to obtain the factored form of the trinomial.

Perfect Square Trinomial: Factor Completely 3×3 12×2 18x

A perfect square trinomial is a trinomial that can be expressed as the square of a binomial. In other words, it is a trinomial of the form (ax + b)2, where a and b are constants.

Determining if a Trinomial is a Perfect Square Trinomial

To determine if a trinomial is a perfect square trinomial, you can use the following steps:

• Check if the first and last terms are perfect squares.
• Check if the middle term is twice the product of the square roots of the first and last terms.

If both of these conditions are met, then the trinomial is a perfect square trinomial.

Factoring a Perfect Square Trinomial

To factor a perfect square trinomial, you can use the following formula:(ax + b)2 = a2x2 + 2abx + b2For example, to factor the trinomial 9×2 + 12x + 4, we can use the following steps:

• Check if the first and last terms are perfect squares. The first term, 9×2, is a perfect square because it is the square of 3x. The last term, 4, is also a perfect square because it is the square of 2.
• Check if the middle term is twice the product of the square roots of the first and last terms. The square root of 9×2 is 3x, and the square root of 4 is 2. Twice the product of 3x and 2 is 12x, which is the middle term.

• Therefore, the trinomial 9×2 + 12x + 4 is a perfect square trinomial. We can factor it as (3x + 2)2.

Difference of Squares

A difference of squares is a trinomial that can be factored as the product of two binomials. The first binomial is the sum of the first and last terms of the trinomial, and the second binomial is the difference of the first and last terms of the trinomial.

To determine if a trinomial is a difference of squares, check if the first and last terms are perfect squares and if the middle term is twice the product of the square roots of the first and last terms. If these conditions are met, the trinomial is a difference of squares.

Factoring a Difference of Squares

To factor a difference of squares, use the following formula:

$$a^2

• b^2 = (a + b)(a
• b)$$

where aand bare the square roots of the first and last terms of the trinomial, respectively.

Sum and Difference of Cubes

A sum of cubes is a trinomial that can be expressed as the sum of two cubes, while a difference of cubes is a trinomial that can be expressed as the difference of two cubes.

Factoring Sum and Difference of Cubes

To factor a sum or difference of cubes, we can use the following formulas:

• Sum of Cubes: a³+ b³= ( a+ b)( a²– ab+ b²)
• Difference of Cubes: a³– b³= ( a– b)( a²+ ab+ b²)

To determine if a trinomial is a sum or difference of cubes, we can check if it fits the pattern of either formula. If it does, we can factor it accordingly.

Top FAQs

What is factoring completely?

Factoring completely involves expressing an algebraic expression as a product of its irreducible factors. It reduces complex expressions into simpler forms, making them easier to analyze and solve.

Why is factoring completely important?

Factoring completely has numerous applications in mathematics. It helps simplify expressions, solve equations, find roots and zeros, and understand the behavior of functions.